
As a mathematics teacher, it’s easy to dream about the dynamite lessons you could plan and deliver if only you had a little more time up your sleeve.
But we don’t live in a perfect world. With time at a premium, it’s not always possible to prepare cutting-edge resources and coordinate lengthy student-focused activities.
That doesn’t mean your teaching has to suffer. There’s still plenty you can do to drive engagement and foster conceptual understanding in your day-to-day lesson.
Here are 6 simple yet effective instructional strategies for mathematics that you can weave into your daily practice.
1. Make conceptual understanding a priority
For students to use mathematics flexibly and grapple with complex problems, they need more than facts and procedures.
They need a deep understanding of mathematical concepts themselves.
Here’s how you make conceptual understanding a priority in your classroom:
Use visual strategies
Making a concept visual allows students to see how an abstract concept translates to a physical scenario. Use illustrated problems or hands-on activities, and encourage students to use visual methods of their own (e.g. drawing) when solving problems.
Seeing a problem in different ways also builds the brain’s neural networks, increasing understanding and retention.
Use the schema approach
The schema is the underlying pattern behind a mathematical concept. All subtraction problems, for example, revolve around a certain amount of something being taken away from an original amount. Once students grasp the schema, they’ll be able to notice it in a diverse array of different problems.
To do this, put similar word problems (e.g. addition ones) side by side and help students discover what they have in common. See if they can express this in words that might apply to other problems of the same type.
Explicitly teach the mathematics vocabulary of a concept
Show the different ways a concept might be expressed in words. Addition, for example, might be expressed as two quantities “together” or a “combined amount”. Once they broaden their math(s) vocabulary, they’ll be able to use concepts much more flexibly.
- Here are some fun ways to build mathematical vocab:
- Display words on posters around the classroom.
- Have students bookmark a mathematics dictionary on their browser (link to ours).
- Have students write down a mathematical word, which they then describe to a partner without using the word itself. The partner has to guess which mathematical concept it is.
2. Set meaningful homework that builds on class learning
You hear the bell ring and – in a last-minute panic – yell out an order to complete exercise 15.2, odd number questions, and every second column.
We’ve all been there. After all your lesson planning, meaningful homework sometimes slips through the cracks.
But if you integrate homework into your lesson plans, you’ll find it much easier to set activities that build deep understanding and engage students that much more.
Think about how your students might reflect on or connect new knowledge at home, rather than just blindly practicing a process.
For example, they could:
- Teach someone else in the family about what they’ve learned
- Find a real-life application of the lesson’s concept somewhere in the home
- Put theory into practice with a hands-on activity (e.g. creating a timetable, cooking)
- Ask qualitative or ‘value’ questions of family members where appropriate.
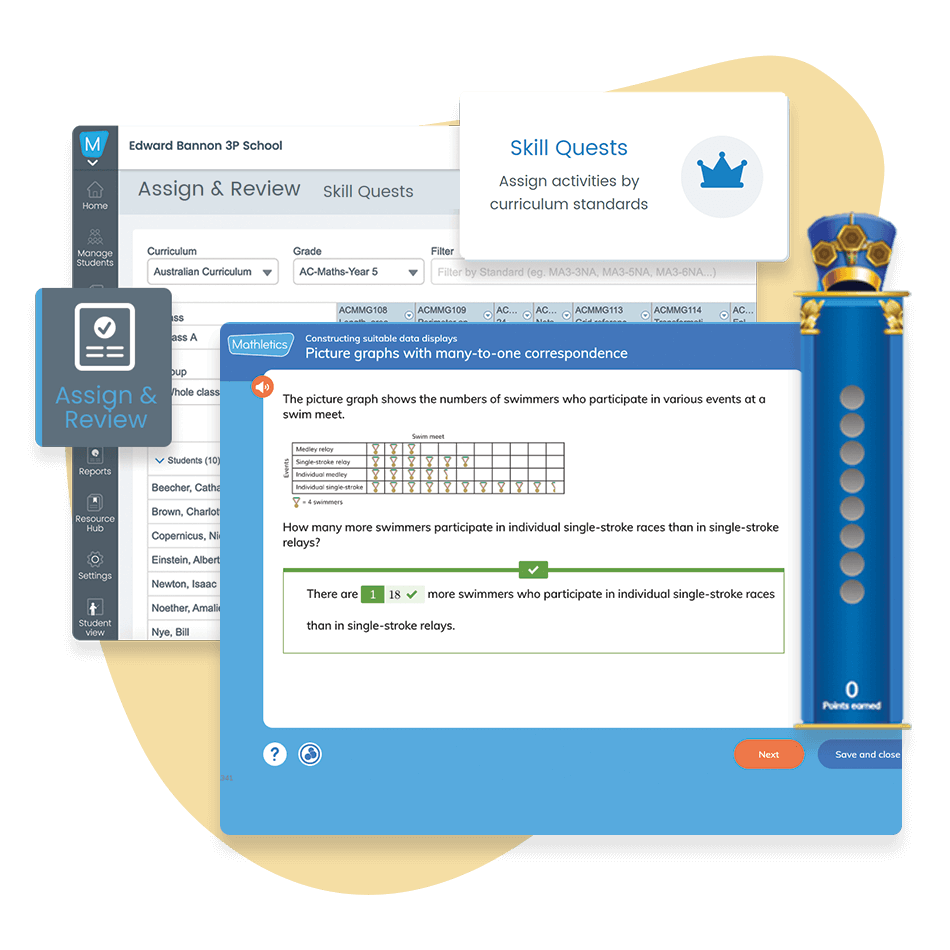
Mathletics has targeted curriculum activities to ensure your students are progressing within their zone of learning
3. Use cooperative learning strategies
Cooperative learning has three major benefits in mathematics:
- It encourages students to express their mathematical thinking, which in turn gives them greater clarity of thought and self-awareness of their own problem-solving strategies.
- Communicating with others exposes students to different mathematical approaches, which they can use to think more flexibly.
- It mirrors the way mathematics is done outside the classroom, where people with different strengths work together to solve challenging real-world problems.
Here’s how you can use cooperative learning strategies effectively in your classroom:
The “puzzle pieces” approach to group work
Use the “puzzle pieces” approach, where each learner is given a unique piece of information to share with the rest of the group to solve a problem. That way every student has to get involved, and everyone has something to contribute regardless of ability level. (Tip: find some examples of puzzle piece activities in our article on math enrichment.)
Take time to reflect
Build-in reflection time after a collaborative activity for students to reflect on what worked, which strategies they found helpful, and how being exposed to other ways of reasoning has made them think differently.
Be strategic when allocating groups
A mix of ability levels will mean top-level students can consolidate their understanding by guiding the activity, while others can learn from more experienced peers. That way, students never miss out on learning, even if they’re always helping others (in fact, research suggests that teaching others yields the highest retention of any strategy).
4. Use strategic questioning
Strategic questions can help turn a regular ‘chalk and talk’ lesson into a deep learning experience, or scaffold learning acting as students advance into more challenging territory. Try using open-ended questions such as:
“Tell me how you solved that”
Instead of congratulating a student when they get an answer correct and moving on, ask them to communicate their approach. This achieves two things:
- The student is encouraged to reflect on their own thought process in detail. Instead of just “doing the math(s)” automatically, they’ll understand exactly the steps they took – and begin to see how these might be adapted to future, more challenging problems.
- Other students get the opportunity to see how they could have solved the problem, even if they struggled to do so originally.
“Is there any other way of solving this?”
Asking students to elaborate on different approaches to the same question highlights that there is no single, correct way of doing the mathematics. Moreover, students might discover some new mental mathematics tips or strategies from their peers that they can use in future activities.
“Does this problem remind you of anything else we’ve done before?”
Before students start shrugging their shoulders in response to an unfamiliar problem, ask them if it reminds them of anything they’ve done before.
They’ll start to notice previously encountered concepts underneath the surface. This habit of checking for familiarity is what produces flexible and agile mathematical thinkers.
“Where could you use this…” or “where would you see this used in the real world?”
These questions drive home the relevance of the learning. Instead of procedural knowledge alone, students will also come away with an understanding of how to apply that knowledge.
5. Focus on real problem-solving and reasoning
In the world beyond the classroom, mathematics takes the form of complex problems as opposed to straightforward questions with just one answer. For this reason, the most effective instruction equips students with the problem-solving and reasoning skills they’ll need for real life.
But this doesn’t mean an arbitrary word problem with apples and oranges. Instead, the best problems are real. That means they:
- Are open-ended. Instead of funnelling students to a particular solution, keep it open to different approaches.
- Approximate relevant real-world scenarios, or (even better) invite students to get hands-on with real items.
- Encourage students to collaborate and explore different perspectives.
- Don’t spell out exactly what students need to do. Let them trial different procedures until they settle on a strategy that works instead.
Use these examples of great problem-solving tasks.
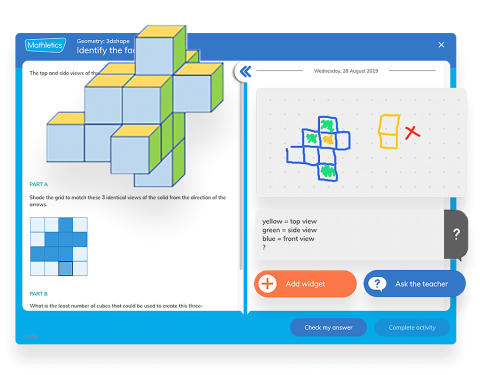
Get access to 700+ unique problem solving and reasoning activities with a free trial
6. Use mixed modes of assessment
A variety of formative and summative assessment types will allow you to:
- Assess conceptual learning, as well as fact recall
- Build on what students know, instead of just assessing what they don’t
- Notice gaps in the learning before the final test
Here are some assessment types that provide an alternative to standard timed testing:
- Reflections
- Portfolios
- Peer assessments
- Interviews
- “Teach the class” activities
Tip: Learning doesn’t have to cease for assessment to take place. Try and integrate the two, e.g. by assessing students’ collaborative abilities while they do a group task.

Join millions of students across the globe to celebrate World Maths Day!
More instructional strategies for mathematics
Mathematics activities
Concept-specific instructional strategies
- How to teach addition
- How to teach multiplication
- How to teach subtraction with regrouping
- How to teach addition with regrouping
Other instructional strategies for mathematics
- Math enrichment strategies
- Strategies to support struggling math students
- Mental math strategies
- Problem-solving strategies










